高中数学难点概念的PCK分析研究
上海市松江区教师进修学院 阮晓明
一、研究的背景与意义
概念是思维的基本形式,数学概念是客观事物中数和形的本质属性的反映.在数学学科中,概念是数学的逻辑起点,是导出数学定理和法则的基础.数学概念的基础性决定了其在数学教学中的特殊地位,国内外数学教育工作者都十分重视数学概念的教学,如匡继昌教授就曾指出:数学概念是数学理论的核心和精华,理解和掌握数学概念是提高教学质量和教学水平的关键.
对于数学概念教学,教师们在长期的教学实践中积累了大量的教学经验和实践案例,有力地支撑着数学概念的课堂教学.但也注意到,在高中数学中还存在着一些重要的数学概念,学生在学习这些概念时普遍感到难以理解和掌握,我们可以称之为难点概念.教师们在难点概念教学之前应进行充分的思考和研究,设计出合理、科学的教学进程,有效地突破难点概念的教学,为提供数学教学质量必要的保证.
二、研究的问题与目标
用统计的方法确定高中数学中的难点概念,提出对难点概念进行PCK分析的方法步骤,对高中数学中主要的十几个难点概念进行深入的PCK分析,探索教学实践的案例研究.
我们认为,难点概念之所以成为教与学中的难点,除了这些概念本身具有高度的抽象性和逻辑系统性外,还与教师的教学准备不够充分有关.一些教师对难点概念所蕴含的数学内涵、课程和教材知识体系缺乏深入研究,对学生学习过程中的经验和困难缺乏了解,对典型教学方法和教学案例的占有还不够丰富.要解决这些问题,对难点概念进行PCK分析是一条有效的途径.探索对难点概念进行PCK分析的方法步骤,对高中数学中主要的十几个难点概念进行深入的PCK分析,并提供相应的课堂教学实践案例,为教师突破对这些概念的教学难点提供参考
三、研究的过程与方法.
1、高中数学难点概念的确定与成因分析
与通常的研究者仅凭个人经验主观地圈定哪些概念属于难点概念不同,我们采用对师、生进行问卷调查的客观方法,来确定师、生心目中高中数学最难的概念.并提出以统计的方法定义高中数学难点概念.为此,我们对上海版教材中所有给出了定义的数学概念进行疏理,并绘出高中数学概念逻辑关系结构总图.
在此基础上设计“高中数学十大难点概念问卷调查表”,分别对上海市松江区全体高中数学教师、上海市松江区的各类学校的部分高三年级学生进行问卷调查,用统计的方法确定师生认为的高中数学难点概念,并对其难点的成因进行分析.
2、对数学难点概念进行PCK分析的方法
根据PCK理论,结合教师对概念教学的课堂实践经验,我们对难点概念的PCK从以下几个方面进行分析:
(1)概念的数学学科知识分析
(2)概念的表征分析
(3)概念的学习经验分析
(4)概念的学习障碍与解决对策分析
(5)概念的教材分析
3、高中数学主要难点概念的PCK分析
我们从调查统计得到的难点概念中挑选出十三个核心概念,按照确定的难点概念PCK分析方法,逐一进行PCK分析研究,形成高中数学主要难点概念的PCK分析系列研究报告.
4、高中数学主要难点概念的教学案例研究
在对十三个难点概念进行PCK分析的基础上,设计出相应的教案开展课堂实践,形成高中数学主要难点概念教学案例集.
四、研究的主要成果
1、高中数学概念体系的疏理
通过对教材的全面疏理,我们统计出高中数学教材共有381个新的概念,其中在基本内容中有305个概念,拓展内容中有76个概念.我们以概念编号、概念的名称、概念的定义(文字表述)、概念的符号表示为表头,编制出高中数学概念汇总表.我们还利用Freemind(思维导图)软件工具,绘制出高中数学概念逻辑关系结构图.并验证了本套教材的概念体系结构较完整、逻辑体系清晰.高中数学概念汇总表和逻辑结构图的绘制,有助于师生进一步明确概念间的内在联系,对提高数学概念教与学的成效具有积极意义,受到了师生的欢迎.
2 、高中数学难点概念的确定与成因
(1)高中数学前20大难点概念排序
通过上海市松江区全体高中数学教师(有效样本容量为85)和各级各类学校学生(有效样本容量为410)的调查和统计分析.在对教师进行的调查中,我们对不同性别(男教师、女教师)、不同教龄(0-5年、6-10年、11-25年、25年以上)、不同职称(二级教师、一级教师、高级教师)、当前任教不同年级(高一年级、高二年级、高三年级)的教师群体分别进行统计.我们还对不同性别(男生、女生)、不同学校(市示范性高中、区示范性高中、普通高中)的学生分别进行统计.其中的高中数学前20大难点概念排序如下.
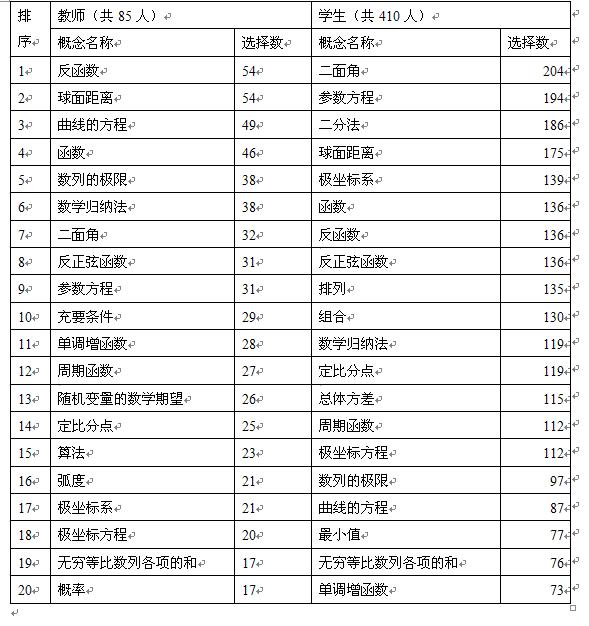
(2)各难点概念的成因分析
我们对统计得到的前二十个难点概念的学习困难成因进行了分析,节选如下:

(3)调查分析的主要结论
①师生心目中的高中数学难点概念具有较高的集中度
②难点概念大多是高中数学中的核心概念
③难点概念的成因主要有:
概念本身的原因:
部分概念抽象层级多,抽象思维和逻辑思维要求高,表征方法少,具体化、形象化困难,理解难度大.
教材编写中的问题:
部分概念定义的文字表述过长、语言枯燥、符号抽象难懂;教材中对概念的形成提供的感性材料不够充分;巩固概念的配套练习不够恰当;教学课时安排过于紧张,学生缺乏深入理解所必须的时间.
教师教学中的问题:
对所引入概念的必要性(背景)阐述不够重视;对概念本质属性的剖析不够到位,没有从文字叙述、图形、数学符号等多角度地揭示概念的内涵和外延;对概念辨析的教学环节重视不够,普遍存在以解题代替巩固练习的现象.
学生学习中的问题:
不能理解部分概念学习的必要性,学习动力不足;上位概念理解不深、固定点知识薄弱;语言转换能力缺乏,难以用自己的语言表述概念;表征方法少,缺乏原型和样例支撑;不清楚相关概念的内在联系,无法形成恰当的概念网络结构.
3、难点概念PCK分析的方法步骤
通过研究,我们认为对高中数学难点概念PCK分析的方法步骤细化如下:
(1)概念的数学学科知识分析
①定义的文本解读:比较分析国内各种版本教材对同一概念所下定义的异同.
②相关概念的溯源:对定义所涉及到的上位概念进行溯源.
③定义的逻辑分析:定义方法的分析;在高中阶段下位概念体系的疏理.
(2)概念的表征分析
对概念的一些主要表征形式进行列举和分析.
(3)概念的学习经验分析
①回顾概念在数学中的发展史.
②分析学生已有的与此概念相关的学习经历.
(4)概念的学习障碍与解决对策分析
分析学生在学习概念时可能遇到的主要障碍和错误类型,并提出相应对策.
(5)概念的教材分析
分析上海版教材在涉及此概念教学内容的结构编排和教学要求.
4、高中数学主要难点概念的PCK分析系列研究报告
我们从高中数学前二十个难点概念中选取十三个概念进行PCK分析研究,各具体概念分别形成了7000~12000字的PCK分析,形成了高中数学主要难点概念的PCK分析系列研究报告,其中“函数”概念的PCK分析报告的简要形式如下:
⑴函数概念的数学学科知识分析
①各种版本教材中函数概念的定义都具有文字表述长、数学符号多、涉及的上位概念多等特点,并一次性地同时给函数、自变量、因变量、定义域、函数值、值域等多个概念下定义,函数概念本身就较为复杂.
②函数概念采用了属加种差的定义方法.在上海版教材中,函数概念的属概念是“对应”,三个种差分别为:建立对应的两个集合都是非空数集、对应的象存在、对应的象唯一.教材未对“函数”的上位概念“对应”下过定义,学生只能对“对应”概念“望文生义”,实属教材编写中的问题.
③函数是基本核心概念,教材中以此为基础的下位概念多达34个.
⑵函数概念的表征分析
函数概念的表征方式主要有:①符号表征、②图形表征、③表格表征、④集合箭图表征、⑤函数机器表征等
⑶函数概念的学习经验分析
①在数学史中回顾函数概念的发展史.
自1673年,莱布尼兹首次使用“function” (函数)表示“幂”以来,数学史上对函数的概念理解发生重大改变的就有10多次,教材主要采用的是19世纪形成的“对应关系”说.
②学生学习经验分析
在小学阶段,教材中已出现过函数机器图.在初中阶段,通过行程问题、数学面积公式、程序计算等具体问题,多次体验了某些运动变化过程中变量间的相互依赖关系的模型.在初中函数概念的学习时,学生在明确了“变量”与“常量”的概念,并学习了初中教材中函数的“变量说”定义.
⑷函数概念的学习障碍分析
学生在函数概念学习中的主要学习障有:①理解“变量”概念时的障碍;②理解函数符号时的障碍;③理解函数表示法时的障碍;④理解函数图像时的障碍;⑤函数与方程概念混淆时产生障碍等.
⑸“函数的概念”教材分析
上海版教材(高中数学高一年级第一学期第3章第1节)
①知识准备:在初中八年级(上)第18章安排了“正比例函数与反比例函数”、初中八年级(下)第20章安排了“一次函数”、初中九年级(上)第26章安排了“二次函数”,高中一年级第1章安排了“集合和命题”、第2章安排了“不等式”,为高中函数概念的学习作了较充分的准备.
②引入编排: 从“喷水池喷出的水的轨道”和“出租车乘车费与行车里程关系”这两个实际问题引入,回顾初中阶段学过的正反比例函数、一次函数、二次函数也都是这种 与 的对应关系.
③定义编排:给出函数的定义叙述,未作进一步解释.
④例题编排:安排了3道例题.
⑤解释说明:教材以“简介”、“注意”、“问题”等形式介绍了数学家笛卡尔、求函数定义域的思、分段函数的定义、函数三种表示法各自的优点等进行了说明.
⑥练习编排:共安排了5道课堂练习.
⑦习题编排:习题分A、B两组共10题,其中A组6题,B组4题.
高中数学主要难点概念的PCK分析系列研究报告目录如下:
(1) “充要条件”概念PCK分析研究
(2) “函数”概念PCK分析研究
(3) “单调函数”概念PCK分析研究
(4) “反函数”概念PCK分析研究
(5) “对数”概念PCK分析研究
(6) “周期函数”概念PCK分析研究
(7) “反正弦函数”概念PCK分析研究
(8) “数学归纳法”概念PCK分析研究
(9) “数列的极限”概念PCK分析研究
(10) “算法”概念PCK分析研究
(11) “曲线与方程”概念PCK分析研究
(12) “球面距离”概念PCK分析研究
(13) “概率”概念PCK分析研究
5、高中数学主要难点概念教学案例集
在对十三个难点概念分别进行PCK分析的基础上,结合对高中数学难点概念的调查和难点成因分析,我们对这些概念的教学进行了实践研究,形成了十九个教学案例
(1) “充要条件”概念教学案例
(2) “函数”概念教学案例
(3) “单调函数”概念教学案例
(4) “反函数”概念教学案例
(5) “对数”概念教学案例
(6) “周期函数”概念教学案例
(7) “反正弦函数”概念教学案例
(8) “数学归纳法”概念教学案例
(9) “数列的极限”概念教学案例
(10) “算法”概念教学案例
(11) “曲线与方程”概念教学案例
(12) “球面距离”概念教学案例
(13) “概率”概念教学案例
五、研究的创新之处
1、提出难点概念的统计定义,确定了高中数学的前二十个难点概念,并进行了归因分析;
2、提出对数学难点概念进行PCK分析的方法步骤;
3、制作“高中数学概念汇总表”和“高中数学概念逻辑结构图”;
4、完成高中数学主要难点概念的PCK分析系列研究报告;
5、完成高中数学主要难点概念教学案例集.
参考文献:
[1]. 匡继昌.如何理解和掌握数学概念的教学实践与研究[J].数学教育学报,2013,22(6):74-78.
[2]. 中华人民共和国教育部. 普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
[3]. 十三院校协编组.中学数学教材教法[M]. 北京:高等教育出版社.1981.
[4]. 袁震东. 高级中学课本—数学 [M].上海:上海世纪出版股份有限公司、上海教育出版社2008.
[5]. Shulman,L.S.Those who understand knowledge growth in teaching[J].Educational Researcher,1986,15(2):4-14.
[6]. 张奠宙,李士锜,李俊.数学教育学导论[M].北京:高等教育出版社.2003:186—190.
[7]. 李求来,昌国良.中学数学教学论[M].湖南师范大学出版社,2006:39-43.
[8]. 苗均台.数学教学应关注学生学习的过程.陕西教育[J],2008,10.
[10].李士锜.PME:数学教育心理[M].上海:华东师范大学出版社,2001:103一119.
[11].徐利治,张鸿庆.数学抽象度概念与抽象度分析法.数学研究评论[J],1985,(5):135-140.
[12].喻平.数学学习心理的CPFS结构理论与实践[M]南宁:广西教育出版社,2008:102-103.
[13].李善良.现代认知观下的数学概念学习与教学理论研究[D].江苏:南京师范大学.2002:78.
[14].张奠宙,李士锜,李俊.数学教育学导论[M].北京:高等教育出版社.2003:181.
[15].涂荣豹.数学教育心理学[M].南京:南京师范大学出版社,2003:275.